Finite-Size Effects in Jammed Configurations

Investigating Finite-Size Effects in Jammed Systems

Jamming criticality encompasses a range of systems, from glasses and colloids to foams and neural networks. A notable characteristic of this phenomenon is the emergence of power-law distributions in small interparticle forces (f) and gaps (h).

Recent mean-field (MF) theories predict these distributions’ exponents in the limit of infinite spatial dimensions (d \to \infty). Surprisingly, these predictions align closely with numerical results in two and three dimensions. Stability considerations further suggest that these systems are marginally stable at the jamming threshold.

Key Findings from Recent Research

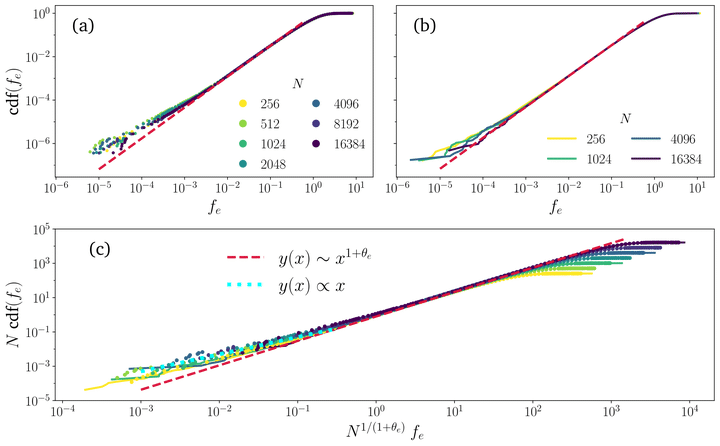
A comprehensive study by Charbonneau et al. examined finite-size scaling in various particle-based jamming models. Their analysis revealed:

• Pronounced Finite-Size Effects in Gaps: The distribution of gaps (h) exhibits more significant finite-size effects than that of forces (f), indicating longer-range correlations for gaps.

• Consistency Across Models: Except for near-crystalline packings, all models studied showed remarkable agreement with MF predictions, reinforcing the robustness of these theoretical frameworks.

• Secondary Linear Regime: Both force and gap distributions display a secondary linear regime in their tails, a feature attributed to the near-isostatic nature of the configurations.

Implications for the Jamming Universality Class

These findings enhance our understanding of the jamming transition, highlighting the influence of system size on critical properties. By delineating the finite-size effects, this research offers deeper insights into the universal aspects of jamming phenomena.

For a detailed exploration, refer to the full study: Finite-Size Effects in the Microscopic Critical Properties of Jammed Configurations.