Hierarchical Jamming

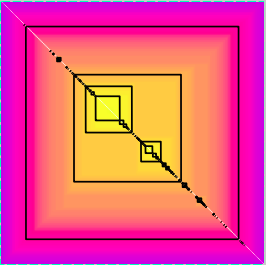
Hierarchical Structure in Jamming Energy Landscapes

Jammed systems, such as glasses and granular materials, exhibit complex energy landscapes that influence their physical properties and behaviors. Recent research has demonstrated that these landscapes possess a hierarchical and ultrametric organization, even in finite three-dimensional systems.

In the study “Jamming Energy Landscape is Hierarchical and Ultrametric” by R. C. Dennis and E. I. Corwin, the authors investigated the energy minima of jammed configurations. By analyzing the distances between nearby minima in configuration space, they constructed a metric that reveals a clear hierarchical structure, indicative of an ultrametric space. This finding provides direct evidence for a marginal phase along the zero-temperature jamming line.

Key Findings

• Ultrametricity in Finite Systems: The study confirms that the ultrametric organization of energy landscapes, previously predicted by mean-field theories, persists in finite, out-of-equilibrium three-dimensional systems.

• Hierarchical Energy Minima: The researchers identified sets of nearby minima in configuration space, demonstrating a nested, hierarchical arrangement.

• Implications for Marginal Stability: The hierarchical structure of the energy landscape supports the existence of a marginally stable phase in jammed systems at zero temperature.

These insights enhance our understanding of the complex energy landscapes in jammed systems and have implications for the study of glasses, granular materials, and other disordered systems.

For a comprehensive exploration of this research, refer to the full article: “Jamming Energy Landscape is Hierarchical and Ultrametric”.